Kaju Yamaka • 26 de fev, 2024

Matemática Básica

Dúvidas Frequentes de Aritmética Elementar

Leia mais: Introdução às Frações

Quais são os nomes dados aos termos de uma fração?

Uma fração é formada por dois inteiros separados por uma barra de vinculum. O número de cima é o numerador e o debaixo é o denominador.

Como se chama o número que está acima do traço da fração?

Numerador.

O que indica o denominador da fração?

O denominador indica em quantas partes iguais o inteiro deve ser dividido.

Como podemos localizar uma fração na reta numérica?

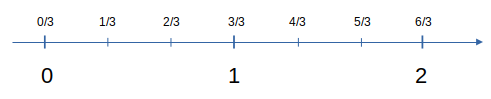
Divida o intervalo unitário pelo número expresso pelo denominador da fração. Conte a partir do zero o número de partes correspondente o numerador da fração.

Segue exemplo da localização de vários múltiplos de 1/3 na reta numérica:

O que é uma fração própria?

Fração própria é quando o numerador é menor que o denominador.

Quando a fração é imprópria?

Fração imprópria é quando o numerador é maior que o denominador.

Como saber se a fração é aparente?

Fração aparente é quando o numerador é um múltiplo do denominador.

O que é uma fração mista?

Fração mista é uma notação alternativa em que a parte inteira é escrita fora da parte fracionária. Exemplos:
- 1¼ , um inteiro e um quarto
- 5¾ , cinco inteiros e três quartos
- 2⅗ , dois inteiros e três quintos

Como transformar uma fração em um número misto?

Faça a divisão inteira do numerador pelo denominador. O quociente inteiro é a parte inteira da fração mista. O resto inteiro é o numerador. E o denominador da fração mista é o mesmo que da fração ordinária.

Como se faz uma fração equivalente?

Multiplique tanto o numerador quanto o denominador por um mesmo inteiro. O resultado será uma fração equivalente a fração original.

Como fazer para simplificar uma fração?

Encontre um número inteiro que divida simultaneamente tanto o numerador quanto o denominador. O resultado será uma fração equivalente a original mas com termos menores (ie: simplificados).

Quais são as frações irredutíveis?

Frações irredutíveis são frações que não tem como encontrar frações equivalentes mais simples. Isso acontece quando não existe um número inteiro que divida simultaneamente tanto o numerador quanto o denominador.

Como transformar as frações irredutíveis?

Não tem como simplificar ainda mais as frações irredutíveis. No entanto, é possível encontrar frações equivalentes com termos maiores.

Como saber se uma fração é igual à outra?

Simplifique as frações até chegarem em suas formas irredutíveis. Nesse caso, se os termos das frações forem exatamente os mesmos, então as frações são equivalentes. Caso contrário, as frações não são equivalentes (ie: não são iguais).

Dúvidas e Comentários

Continua com dúvidas? Quer fazer um comentário?

Envie um email para: kaju.yamaka@gmx.com

Voltar para: