Kaju Yamaka • 30 de dez, 2023

ENEM 2023

MATEMÁTICA E SUAS TECNOLOGIAS

QUESTÃO 142

Sejam a, b e c as medidas dos lados de um triângulo retângulo, tendo a como medida da hipotenusa. Esses valores a, b e c são, respectivamente, os diâmetros dos círculos C₁, C₂ e C₃, como apresentados na figura.

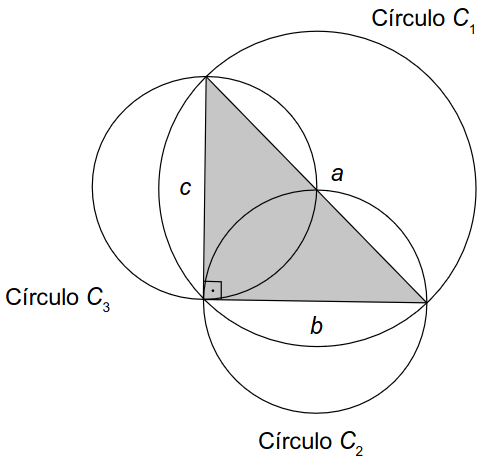
Observe que essa construção assegura, pelo teorema de Pitágoras, que área (C₁) = área (C₂) + área (C₃).

Um professor de matemática era conhecedor dessa construção e, confraternizando com dois amigos em uma pizzaria onde são vendidas pizzas somente em formato de círculo, lançou um desafio: mesmo sem usar um instrumento de medição, poderia afirmar com certeza se a área do círculo correspondente à pizza que ele pedisse era maior, igual ou menor do que a soma das áreas das pizzas dos dois amigos. Assim, foram pedidas três pizzas. O professor as dividiu ao meio e formou um triângulo com os diâmetros das pizzas, conforme indicado na figura.

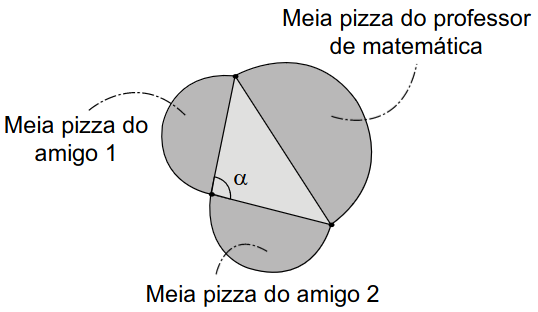
A partir da medida do ângulo α, o professor afirmou que a área de sua pizza é maior do que a soma das áreas das outras duas pizzas.

A área da pizza do professor de matemática é maior do que a soma das áreas das outras duas pizzas, pois

(A)   0° < α < 90 °

(B)   α = 90°

(C)   90° < α < 180 °

(D)   α = 180°

(E)   180° < α < 360 °

Gabarito

(C)

Resolução

Pela lei dos cossenos sabemos que:

a² = b² + c² - 2.b.c.cosα

Usando a fórmula da área do círculo para os círculos C₁, C₂ e C₃ temos:

S₁ = π.a²/4 , S₂ = π.b²/4 , S₃ = π.c²/4

Isolando os lados a, b e c temos:

a² = 4.S₁/π , b² = 4.S₂/π , c² = 4.S₃/π

Inserindo essas fórmulas na lei dos cossenos obtemos:

4S₁/π = 4S₂/π + 4S₃/π - 2bc.cosα

S₁ = S₂ + S₃ - bc.π/2.cosα

bc.π/2.cosα = S₂ + S₃ - S₁

Sabemos que a área da pizza do professor é maior que a soma das outras duas:

S₁ > S₂ + S₃   => S₂ + S₃ - S₁ < 0

Portanto:

bc.π/2.cosα < 0

cosα < 0

A única opção que satisfaz essa condição é 90° < α < 180 ° .

Dúvidas e Comentários

Continua com dúvidas? Quer fazer um comentário?

Envie um email para: kaju.yamaka@gmx.com